Survey Questions (Part 3)

The meaning of “free time” is pretty strange for a professor, since all your time is basically “free”. You have remarkably few real requirements on your time (other than showing up for class a couple times a week every other semester, and filing an annual report once a year), and can mostly choose how you want to spend your time.

How you might view things more normally, one’s view of “free time” changes a lot after having a family. Before that, I would have considered my teaching and research work as the main thing I do, and the time I’m not doing that as “free time”, which I would mostly spend playing and watching soccer, music, and mostly bad TV shows.

Now, I view the main things I do as revolving around my children (4-year old daughter and 1 ½-year old son), and can mostly schedule the rest of my life around that (one of the perks of being a professor, instead of having a real job!). I do get to do lots of fun things with the kids but don’t really consider that “free time” in the traditional sense.

Great question!

Since its been a while, here’s the picture from Class 1:

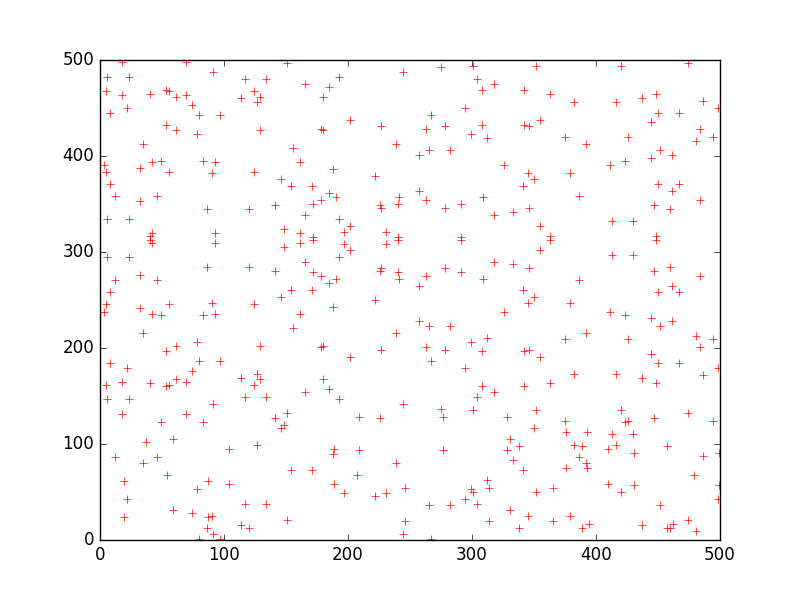
It was generated by this (very ugly and brute force) python code:

import numpy as np
import matplotlib.pyplot as plt

def ellip_curve():
    x = np.arange(-2, 10, 0.1);
    y = np.sqrt(x ** 3 + 7)
    plt.plot(x, y)
    plt.show()

def ellip_curve_field():
    xpoints = []
    ypoints = []
    G = 629
    for x in range(500):
        for y in range(500):
            if y ** 2 % G == (x ** 3 + 7) %  G:
                xpoints.append(x)
                ypoints.append(y)
    plt.plot(xpoints, ypoints, marker='+', linestyle='none', color='r')
    plt.show()

ellip_curve_field()

I picked 629 just because its one of my favorite numbers, but the fact that is has two large factors (17 * 37) makes it produce a less regular graph than we would get for a more divisible number. For example, here is the graph for modulus 628 (2 * 2 * 157):

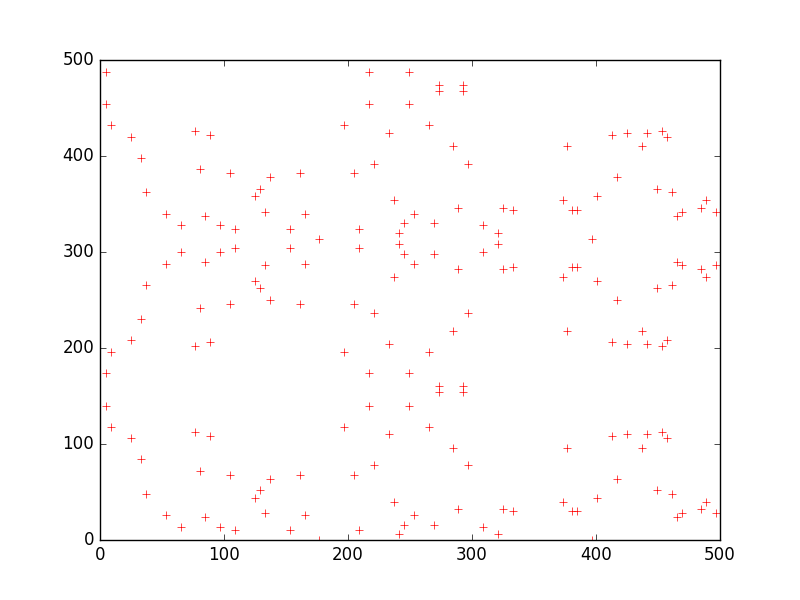
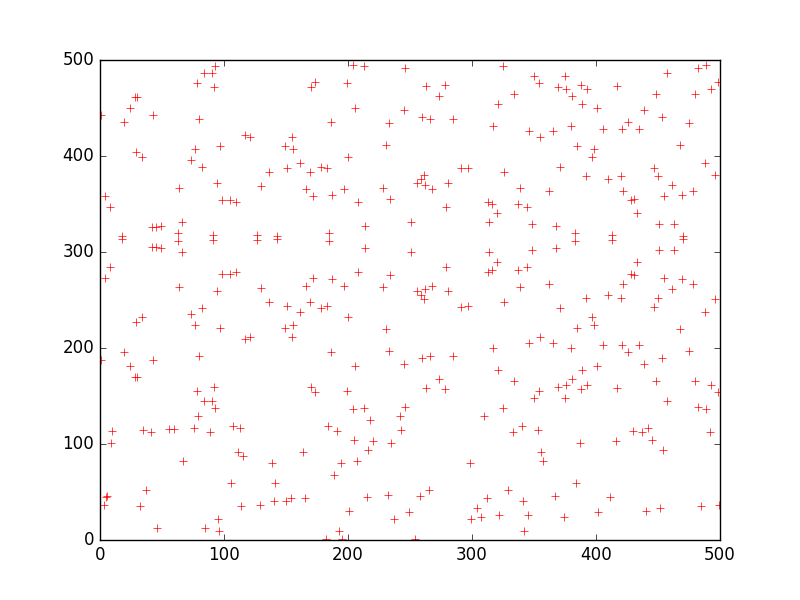
which seems to have more patterns in it than the one for modulus 631 (prime) Of course, the actual modulus values used for cryptosystems like bitcoin are huge prime numbers (2²⁵⁶ - 2³² - 977 for bitcoin’s curve, which is otherwise the same as this one).

When you filled out the survey, about 3 days. Now, its been about 4 weeks. This is my first time teaching cs2102, but I’ve taught lots of other courses.

Yes, I’ll try to keep this in mind and connect things to applications as much as possible, but the gap between some of the theory we will learn and applications is sometimes fairly large (that is, we need to get fairly deep into the theory before we can connect it to applications well). That said, nearly every concept in this class does have clear connections to applications in computing, and we’ll see many examples, and I’m always happy to talk about more in office hours.

My research is in computer security and applied cryptography, which is entirely built on discrete math. I will try to integrate this into some of the lectures, but definitely have some classes toward the end of the semester that get more into how discrete math is essential for cryptography, and maybe even how some of the problems you’re learning about in this class can be used to enable zero-knowledge proofs (that is, proving that you know something without revealing anything about it) and multi-party computation (enabling two people to compute a function together without revealing any information about their inputs).

If you are able to demonstrate good understanding of the key concepts in the course, and ability to use them to solve problems well, you’ll get an A in the class. Working effectively and consistently on the assignments throughout the semester, of course, should help. It is also important to ask for help, focusing on your understanding of concepts, not just on the immediate goal of being able to answer some question on a problem set. Most people will also benefit greatly by finding a study group to work with that works well together, where you are enhancing your learning by explaining things to others, and testing the limits of your understanding by having others question your assumptions and approaches.

This is a math course (hence the name Discrete Mathematics), but also a computer course (hence the course number cs2102). I would claim all the math we do in the class has some significant relevance to computing, but it is also selected partly for relevance to computing and partly for being interesting math (at least in my view, or that of the textbook author’s). I would say the decisions about what to include in the class are based about 50% on relevance to computing and 50% on interesting math (which would mean that something that is highly relevant to computing but uninteresting math would not be covered in favor of something that is less directly relevant to computing but interesting math).

Not for most of them. I understand that it would be very helpful to be able to look at solutions after you try problems yourself. We’ll provide solutions to the problems assigned on problem sets, but if you have other problems that you’ve tried to solve on your own and want to get feedback on your solution or suggestions for a good solution, feel free to send your solution (or attempt and explain what you are trying to do) to me.

I don’t expect this class will be that helpful directly in exploring possible computing careers, but do hope it will give you the background to succeed in many possible careers. What I would say is that if you enjoy and excel and the kinds of problems we do in this class, you are well suited to careers in aspects of computing at the level of designing, reasoning about, and defining systems, as well as in careers where you are reasoning about ideas.

I usually interpret coding as the process of turning a well described algorithm into code in some programming language. This course won’t help too much with that. It is more related to programming, which I view as the process of finding a program that solves some problem. This includes both devising the algorithms and data structures to use, and writing the code to implement them. This course should help you get better at constructing programs and reasoning about whether or not they are correct.

Yes, many times! As one memorable example, in my “Advanced Computer Science” course in high school the teacher assigned us to implement quicksort (I think this was in BASIC). I couldn’t get it to work, and got very frustrated, and refused to turn anything in. Other students turned in obviously broken programs, but got most credit for their attempts. I ended up getting a B in the course as a result, and being very upset about it, but to no avail. I did make my peace with quicksort later, and its now one of my favorite algorithms (and I’ve been privledged to meet its inventor, Tony Hoare, several times and even have dinner with him).

I think this course is probably harder to comprehend than most courses you take, both because of the material and my general approach to teaching. For most students, the material in this course requires you to learn to think in new and unfamiliar ways, and to develop new mental models, not just to learn new things that fit well into your well-developed mental models. My approach to teaching emphasizes challenging students to learn things by exploring things on your own after (hopefully) the right context has been developed to enable this. I believe this is important for really learning things well, as well as developing your abilities to be creative thinkers. But, this is different from what students typically expect and are accustomed to classes where you are given a lot more guidance about what to do and prescribed how to do things.

Yes. There is no requirement to have experience with either Python or Java, but just to have enough familiarity with some programming language to understand programs.

The plan for the first exam is to have an in-class exam, with problems that you should be well prepared to answer if you understand the problem sets. The exam questions will be similar to problem set questions, but less difficult and complex given the limited time available during the exam.

The most direct classes that follow from this one are cs3102 (Theory of Computation) and cs4102 (Algorithms). Many computing courses involve a lot of math including graphics (mostly linear algebra), cryptography (mostly discrete math), and machine learning (includes more continuous math, as well as lots of linear algebra and discrete math). In general, any good math course should help develop your abstract thinking abilities in ways that will be useful in computing, although some will have more direct applications in computing than others.

If the “real world” means a typical software developer in industry, then it is pretty rare for a programmer to need to write a “formal proof” in a mathematical style, but very common for a programmer to need to form a strong argument that convinces others an idea is correct (this is really what a proof is). In terms of mathematical-style proofs, these are very common in computing research and most research papers (even in systems areas like networking and programming languages) include several proofs.

There are lots of great opportunities at UVA. I’ve been impressed with HackCville and the Computer and Network Security Club is great.

Away from Charlottesvile, the Recurse Center is very cool (when I visited it was called Hacker School), and they have students for summer sessions.

Lots of students have great experiences doing research over the summer, and there are many ways for students to get involved in research groups and have paid positions over the summer (including in mine).

I don’t want to mention specific companies for internships publicly here, but there are some that I’ve heard students have great experiences at, and other where the experiences are more mixed. I’m happy to share my thoughts on this privately during office hours (or make an appointment to meet some other time).

Absolutely! Its turtles all the way down.

I haven’t taught this course before, but in general students work hard in my classes and hopefully learn a lot, and most students in my classes end up getting As. I don’t know what the distribution will be for this class (and I don’t assign grades with a target distribution in mind), but I hope to be able to have at least 2/3rds of the class get As (or at least A-s), and the rest all get at least a B (but sometimes there is no way to justify the desired grate).

None are “dropped” per se, but the grades are computed with many different weightings (some of which don’t count the early homeworks heavily, and others which will only count the number of “green” star or better homeworks) and generally the weighting that make your performance look best is the one that will determine your grade. All the homeworks as important for learning the material well, but you shouldn’t be stressed out about getting a low grade on one or two homeworks.