cs2102
Discrete Mathematics
This is a preserved file from cs2102 Fall 2016. An updated version may exist at https://uvacs2102.github.io/

cs2102: Discrete Math (Fall 2016)

Class 11: Strong Induction (Tue, 27 Sep 2016)

Schedule

Problem Set 5 is due Friday at 6:29pm.

Thursday’s Class may include review for Exam 1. Before 6:59pm Wednesday, send me topics you would like to review:

Friday, 3:30pm (Rice Hall Auditorium): Eva Tardos (Cornell University), Learning and Efficiency of Outcomes in Games. (She could definitely help you answer questions 7-9 on PS5!)

Exam 1

Exam 1 will be in class on Thursday, 6 October.

Resources. You will be permitted to use a single paper page of notes that you prepare and bring to the exam. It is fine to collaborate with others to prepare your notes. The page should be no larger than a US Letter size page ($8.5 \times 11$ inches), and you may write (or print) on both sides of the page. No other resources are permitted during the exam.

Content. The problems on the exam will cover material from Classes 1–11, Problem Sets 1–5 (including the provided solutions), and MCS Chapters 1–5. Everything on the exam will be something you have seen in at least two of these (Classes, Problem Sets, and MCS Book), and most of the exam will be things you have seen in all three. If you understand the problems on the problem sets and questions on the class notes well enough to be able to answer similar questions, you should do well on the exam.

The main topics the exam will cover include:

For most students, I believe the best way to prepare for the exam will be to (1) go over the problem sets and their solutions, and make sure you understand well any of the problems you did not get before; (2) go through the questions in the class notes and convince yourself you can answer them well; (3) re-read chapters of the book, solving the associated practice problems, especially for any sections on topics where you had difficulty on the problem sets. If you do #1 and understand well the problems on the problem set, you should be confident you’ll do well on the exam; if you struggled on the problem sets, you would benefit from doing #2 and #3 as well.

See PDF Version for Notes and Questions.

The strong induction example was based on Chapter 10: Induction from the Book of Proof.

Induction Practice

Take-Away Game: start with $n$ sticks; at each turn a player must remove 1, 2 or 3 sticks; player who takes the last stick wins.

  • Prove: for a Take-Away game with any initial number of sticks, $n$, either Player 1 has a winning strategy or Player 2 does.

  • Prove: Player 1 has a winning strategy for a Take-Away game with $n$ sticks, if \bigfillin. Otherwise, Player 2 has a winning strategy.

Strong Induction Principle

Let $P$ be a predicated on $\mathbb{N}$. If

  • $P(0)$ is true, and
  • $(\forall m \in \mathbb{N}, m \le n . P(n)) \implies P(n + 1)$ for all $n \in \mathbb{N}$,

then

  • $P(m)$ is true for all $m \in \mathbb{N}$.

Show that strong induction is not actually stronger than regular induction.

##

Prove that a tree (fully-connected graph with no cycles in it) with $n$ nodes has $n - 1$ edges.

Self-Inverting Relations Challenge Solved! (Sat, 24 Sep 2016)

Challenge 4 has been solved by Henry Spece!

Challenge 4. (From Class 9) How many self-inverting relations, R: Nk → Nk, are there? (Where Nk is the set of all non-negative integers less than k, and a relation is self-inverting if R = R-1.)

Henry’s answer is below:

2n*(n+1)/2

For each element in the domain, the number of “connection” possibilities for that element to each element of the codomain (given that it can either be related or not related to a codomain element) is 2n, where n is the number of codomain elements.

This includes the possibility of the element connecting to itself, because there are two possibilities involving self connection, and 2(n-1) possibilities for connection to non-identical elements. The product of these two results in 2*2(n-1) = 2n.

For each following element in the domain, the relationship with all previous elements which have been assigned relationships is fixed. For example, if element a in the domain is related to element b in the codomain, then element b in the domain must be related to element a in the codomain. This applies equally if element a in the domain is not related to element b in the codomain, because then element b in the domain must also not be related to element a in the codomain, or the relation would not be self-inverting.

All other relationships between our second element and elements of the codomain are still free to change, though, leaving 2n-1 combinations for the second element considered.

This pattern continues n times in total, and by multiplying these possibilities, we get

2n * 2n-1 * 2 n-2 … * 21

Which is the same as 2n + (n-1) + (n-2) + … + 2 + 1.

By reversing the addition sequence we get that the exponent of 2 is the sum of all numbers from 1 to n, which is equal to n*(n+1)/2.

Hence, the number of self-inverting relations for a set of size n must be 2(n*(n+1)/2).

Congratulations to Henry Spece for solving the challenge!

Problem Set 5 (Fri, 23 Sep 2016)

Problem Set 5 is now posted, and is due on Friday, 30 September at 6:29pm.

Class 10: In(tro)duction (Thu, 22 Sep 2016)

Schedule

Problem Set 4 is due Friday at 6:29pm.

Next week, you should finish reading MCS Chapter 5 (Induction). Another presentation of Induction is Chapter 10 from the Book of Proof (you are not required to read this, but it is encouraged and has lots more examples of proofs by induction).

Exam 1 will be in class on Thursday, 6 October.

See PDF Version for Notes and Questions.

Chapter 10: Induction from the Book of Proof

The Onion, Bush Earmarks 1.5 Billion Gold Stars For Education.

Power Sets (continued from Class 9)

The power set of $A$ ($\textrm{pow}(A)$) is the set of all subsets of $A$: $B \in \textrm{pow}(A) \iff B \subseteq A$.

Prove that the size of the power set of a set $S$ with $|S| = N$ is $2^N$.

Proof using Well-Ordering Principle

The goal is to prove for all sets $A$: $|\textrm{pow}(A)| = 2^{|A|}$.

Recall (from Class 9) that $N_k = { n | n \in \mathbb{N} \wedge n < k } $ and $|\mathbb{N}_n| = n$.

Because of the bijection between any set $A$ where $|A| = n$ to $\mathbb{N}_n$, we can prove the general property by showing $\forall n \in \mathbb{N} \ldotp P(n)$ where $P(n) ::= |\textrm{pow}(\mathbb{N}_n)| = 2^n$.

We follow the structure of every well-ordering proof:

  1. Define the set of counterexamples: $$ C ::= { n \in \mathbb{N} | \quad |\textrm{pow}(\mathbb{N}_n)| \neq 2^n } $$
  2. Assume $C$ is $\fillin\fillin\fillin$.
  3. By the well-ordering principle, there must be some smallest element, $m \in C$.

  4. Reach a contradiction: we show that $\fillin\fillin\fillin$ holds.

    • Since $m$ is the smallest element of $C$, $P(n)$ must hold for all $\fillin\fillin\fillin$.
    • We know $P(0)$ is true since $\mathbb{N}_0 = \emptyset$ and $\textrm{pow}(\emptyset) = \fillin\fillin\fillin\fillin$. We have, $|\textrm{pow}(\mathbb{N}_0)| = \fillin\fillin = \fillin\fillin$, satisfying $P(0)$.
    • Thus, $m > 0$. This means $m - 1 \in \mathbb{N}$.
    • So, we know $P(\fillin\fillin)$ holds.
    • Thus, we can construct $\textrm{pow}(\mathbb{N}{m})$ by keeping all the elements of $\textrm{pow}(\mathbb{N}{m - 1})$ and adding each of those elements with $(m-1)$ inserts. More formally, $$ \textrm{pow}(\mathbb{N}m) = \textrm{pow}(\mathbb{N}{m - 1}) \quad \cup \bigcup{S \in \textrm{pow}(\mathbb{N}{m - 1})} (S \cup \fillin\fillin\fillin) $$ The size of this set is $2 |\textrm{pow}(\mathbb{N}{m - 1})|$ since it contains two sets for each set in $\textrm{pow}(\mathbb{N}{m - 1})$ (the original one, and the one with $m-1$ added, which we know is a new set since $m - 1 \notin \mathbb{N}_{m - 1}$).
    • Since $P(m-1)$, we know $|\textrm{pow}(\mathbb{N}{m - 1})| = \fillin\fillin\fillin$. The size of the new set, $|\textrm{pow}(\mathbb{N}{m})| = 2 \cdot 2^{m - 1} = 2^{m}$. This means that $P(m)$ holds.

  5. Hence, $C$ must be empty. We reached a contradiction using the well-ordering principle by showing the $P(m)$ holds for $m \in C$, which must mean the $C$ is empty. If there are no counter-examples, then $P(n)$ holds for all $n \in \mathbb{N}$.

Induction Principle

Let $P$ be a predicated on $\mathbb{N}$. If

  • $P(0)$ is true, and
  • $P(n) \implies P(n + 1)$ for all $n \in \mathbb{N}$,

then

  • $P(m)$ is true for all $m \in \mathbb{N}$.

Template for Induction Proofs

  1. State, “We prove by induction.”
  2. Define a predicate, $P(n)$. This is the induction hypothesis. Our goal is to show that $P(n)$ is true for all $n \in \mathbb{N}$.
  3. Prove $P(0)$ is true. (base case or basis step.)
  4. Prove that $P(n) \implies P(n + 1)$ for every $n \in \mathbb{N}$. (induction step)
  5. Conclude that $P(n)$ is true for all $n \in \mathbb{N}$ by induction.

How is the method of proof by induction principle similar to and different from proof by well-ordering principle?

Induction Practice

Prove the non-negative integers are well ordered by the induction principle.

###

Prove the power set size property, $|\textrm{pow}(A)| = 2^{|A|}$, by induction.

###

Problem Set 3 Comments (Thu, 22 Sep 2016)

The solutions and comments for PS3 are now posted in collab: PDF

You should find your graded assignment as a new PDF attachment with markup on it in collab (if you submitted with teammates, please check with your partners).

The meaning of the scores is the same as for PS1 and PS2. A score of 6 means you got everything we expected out of this assignment, and 5 means you did well for the most part by had some answers that should have been better. Scores above 6 are for excellent work. (In the gradebook, collab sometimes shows the grades scaled by 100 for some buggy reason. Although receiving a score of 100+ is possible in theory, no one received more than 8 points for this assingment. If you see a score about 100, the meaning is that score divided by 100.)

Class 9: Cardinality (Tue, 20 Sep 2016)

Schedule

This week you should finish reading MCS Chapter 4 (section 4.5) and Section 5.1. We will discuss Induction (Section 5.1) next class.

Problem Set 4 is due Friday at 6:29pm.

See PDF Version for Notes and Questions.

Challenge Problem. How many self-inverting relations, R: Nk → Nk, are there? (Where Nk is the set of all non-negative integers less than k, and a relation is self-inverting if R = R-1.)

Relation Practice

The inverse of a relation $R: A \rightarrow B, G \subseteq A \times B$ is defined by reversing all the arrows: $$ R^{-1}: B \rightarrow A, G^{-1} \subseteq B \times A $$

$$ (b, a) \in G^{-1} \iff \fillin\fillin\fillin\fillin $$

What does it mean if $R \equiv R^{-1}$?

Set Cardinality

Finite Cardinality. If $A$ is a finite set, the cardinality of $A$, written $|A|$, is the number of elements in $A$.

Does this definition require adding a new fundamental set operation?

#

Alternate definition: The cardinality of the set $$ N_k = { n | n \in \mathbb{N} \wedge n < k } $$ is $k$. If there is a bijection between two sets, they have the same cardinality.

#

If there is a surjective relation between $A$ and $B$ what do we know about their cardinalities?

##

If there is a surjective function between $A$ and $B$ what do we know about their cardinalities?

If there is a total surjective function between $A$ and $B$ what do we know about their cardinalities?

##

If there is a total surjective injective function between $A$ and $B$ what do we know about their cardinalities?

##

What is the cardinality of $A \cup B$?

#

Power Sets

The power set of $A$ ($\textrm{pow}(A)$)is the set of all subsets of $A$: $$ B \in \textrm{pow}(A) \iff B \subseteq A. $$

Prove that the size of the power set of a set $S$ with $|S| = N$ is $2^N$ using the well-ordering principle. (See MCS 4.5.1 for an alternate proof.)

#

#

Survey Questions (Part 3) (Tue, 20 Sep 2016)

Here’s the third (and final!) installment of responses to questions submitted in the registration surveys (see Part 1 and Part 2 for the earlier responses). If you missed your chance to ask a question on the registration survey, or have new questions now the course is further along, feel free to send them (directly or anonymous is fine if you prefer).

What does Professor Evans do in his free time?
The meaning of “free time” is pretty strange for a professor, since all your time is basically “free”. You have remarkably few real requirements on your time (other than showing up for class a couple times a week every other semester, and filing an annual report once a year), and can mostly choose how you want to spend your time.

How you might view things more normally, one’s view of “free time” changes a lot after having a family. Before that, I would have considered my teaching and research work as the main thing I do, and the time I’m not doing that as “free time”, which I would mostly spend playing and watching soccer, music, and mostly bad TV shows.

Now, I view the main things I do as revolving around my children (4-year old daughter and 1 ½-year old son), and can mostly schedule the rest of my life around that (one of the perks of being a professor, instead of having a real job!). I do get to do lots of fun things with the kids but don’t really consider that “free time” in the traditional sense.

In the lecture, did you choose to mod(629) because its semiprime? And if so is that why the graph became super scattered?
Great question!

Since its been a while, here’s the picture from Class 1:

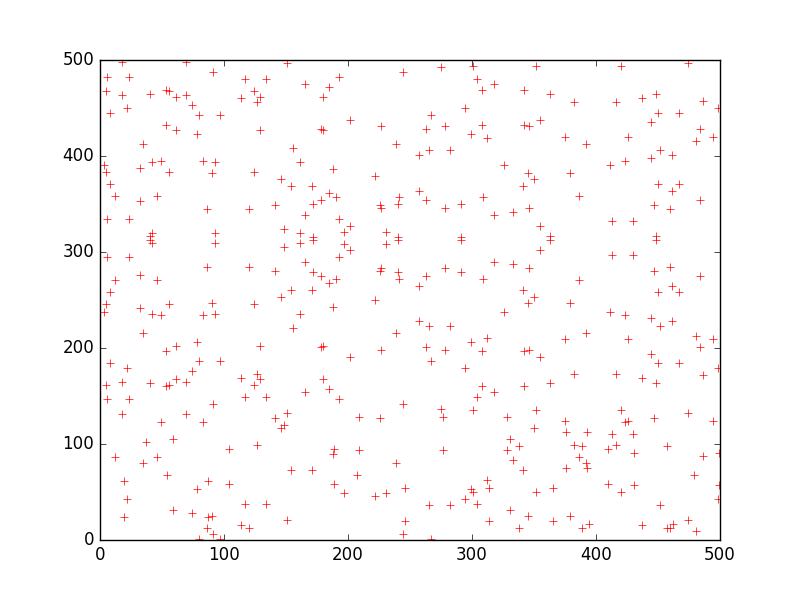
It was generated by this (very ugly and brute force) python code:


import numpy as np
import matplotlib.pyplot as plt

def ellip_curve():
    x = np.arange(-2, 10, 0.1);
    y = np.sqrt(x ** 3 + 7)
    plt.plot(x, y)
    plt.show()

def ellip_curve_field():
    xpoints = []
    ypoints = []
    G = 629
    for x in range(500):
        for y in range(500):
            if y ** 2 % G == (x ** 3 + 7) %  G:
                xpoints.append(x)
                ypoints.append(y)
    plt.plot(xpoints, ypoints, marker='+', linestyle='none', color='r')
    plt.show()

ellip_curve_field()

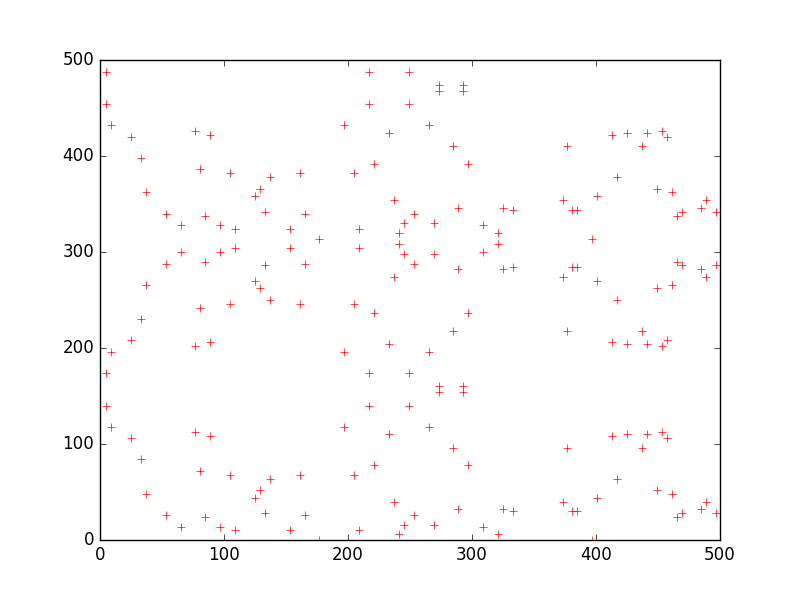
I picked 629 just because its one of my favorite numbers, but the fact that is has two large factors (17 * 37) makes it produce a less regular graph than we would get for a more divisible number. For example, here is the graph for modulus 628 (2 * 2 * 157):

which seems to have more patterns in it than the one for modulus 631 (prime)
Of course, the actual modulus values used for cryptosystems like bitcoin are huge prime numbers (2256 - 232 - 977 for bitcoin’s curve, which is otherwise the same as this one).
How long have you been teaching this course for?
When you filled out the survey, about 3 days. Now, its been about 4 weeks. This is my first time teaching cs2102, but I’ve taught lots of other courses.

More applications of Discrete Math (we talked about encryption, which was really interesting, but I would like to hear about more applications); Professor Evans’ field of research and maybe its relation to Discrete Math
Yes, I’ll try to keep this in mind and connect things to applications as much as possible, but the gap between some of the theory we will learn and applications is sometimes fairly large (that is, we need to get fairly deep into the theory before we can connect it to applications well). That said, nearly every concept in this class does have clear connections to applications in computing, and we’ll see many examples, and I’m always happy to talk about more in office hours.

My research is in computer security and applied cryptography, which is entirely built on discrete math. I will try to integrate this into some of the lectures, but definitely have some classes toward the end of the semester that get more into how discrete math is essential for cryptography, and maybe even how some of the problems you’re learning about in this class can be used to enable zero-knowledge proofs (that is, proving that you know something without revealing anything about it) and multi-party computation (enabling two people to compute a function together without revealing any information about their inputs).

How to get an A?
If you are able to demonstrate good understanding of the key concepts in the course, and ability to use them to solve problems well, you’ll get an A in the class. Working effectively and consistently on the assignments throughout the semester, of course, should help. It is also important to ask for help, focusing on your understanding of concepts, not just on the immediate goal of being able to answer some question on a problem set. Most people will also benefit greatly by finding a study group to work with that works well together, where you are enhancing your learning by explaining things to others, and testing the limits of your understanding by having others question your assumptions and approaches.

How much of this course is pure math, how much is computing, and how much is both? (I apologize for being so vague)
This is a math course (hence the name Discrete Mathematics), but also a computer course (hence the course number cs2102). I would claim all the math we do in the class has some significant relevance to computing, but it is also selected partly for relevance to computing and partly for being interesting math (at least in my view, or that of the textbook author’s). I would say the decisions about what to include in the class are based about 50% on relevance to computing and 50% on interesting math (which would mean that something that is highly relevant to computing but uninteresting math would not be covered in favor of something that is less directly relevant to computing but interesting math).
Are there available solutions to the textbook practice problems?
Not for most of them. I understand that it would be very helpful to be able to look at solutions after you try problems yourself. We’ll provide solutions to the problems assigned on problem sets, but if you have other problems that you’ve tried to solve on your own and want to get feedback on your solution or suggestions for a good solution, feel free to send your solution (or attempt and explain what you are trying to do) to me.
I want to major in CS, but I am not sure I want to go into programming. What can Discrete Mathematics help with in deciding a different career path using a computer science degree?
I don’t expect this class will be that helpful directly in exploring possible computing careers, but do hope it will give you the background to succeed in many possible careers. What I would say is that if you enjoy and excel and the kinds of problems we do in this class, you are well suited to careers in aspects of computing at the level of designing, reasoning about, and defining systems, as well as in careers where you are reasoning about ideas.
How is the course related to coding?
I usually interpret coding as the process of turning a well described algorithm into code in some programming language. This course won’t help too much with that. It is more related to programming, which I view as the process of finding a program that solves some problem. This includes both devising the algorithms and data structures to use, and writing the code to implement them. This course should help you get better at constructing programs and reasoning about whether or not they are correct.
Were you ever discouraged by failure while studying computer science?
Yes, many times! As one memorable example, in my “Advanced Computer Science” course in high school the teacher assigned us to implement quicksort (I think this was in BASIC). I couldn’t get it to work, and got very frustrated, and refused to turn anything in. Other students turned in obviously broken programs, but got most credit for their attempts. I ended up getting a B in the course as a result, and being very upset about it, but to no avail. I did make my peace with quicksort later, and its now one of my favorite algorithms (and I’ve been privledged to meet its inventor, Tony Hoare, several times and even have dinner with him).
Is this course harder to comprehend than other courses and what is the best way to prepare for this course and the exams and home work that will be provided?
I think this course is probably harder to comprehend than most courses you take, both because of the material and my general approach to teaching. For most students, the material in this course requires you to learn to think in new and unfamiliar ways, and to develop new mental models, not just to learn new things that fit well into your well-developed mental models. My approach to teaching emphasizes challenging students to learn things by exploring things on your own after (hopefully) the right context has been developed to enable this. I believe this is important for really learning things well, as well as developing your abilities to be creative thinkers. But, this is different from what students typically expect and are accustomed to classes where you are given a lot more guidance about what to do and prescribed how to do things.
Will I be able to survive with Python experience but no previous Java experience?
Yes. There is no requirement to have experience with either Python or Java, but just to have enough familiarity with some programming language to understand programs.
How are exams like?
The plan for the first exam is to have an in-class exam, with problems that you should be well prepared to answer if you understand the problem sets. The exam questions will be similar to problem set questions, but less difficult and complex given the limited time available during the exam.
How far do you suggest we delve into the world of math in order to become the best computer scientist we can be? What other courses might help broaden our mathematical background in a way that is beneficial to our computer science studies?
The most direct classes that follow from this one are cs3102 (Theory of Computation) and cs4102 (Algorithms). Many computing courses involve a lot of math including graphics (mostly linear algebra), cryptography (mostly discrete math), and machine learning (includes more continuous math, as well as lots of linear algebra and discrete math). In general, any good math course should help develop your abstract thinking abilities in ways that will be useful in computing, although some will have more direct applications in computing than others.
How does the material we have learned so far relate to computer science as a whole? Do programmers in the real world need to know how to write proofs
If the “real world” means a typical software developer in industry, then it is pretty rare for a programmer to need to write a “formal proof” in a mathematical style, but very common for a programmer to need to form a strong argument that convinces others an idea is correct (this is really what a proof is). In terms of mathematical-style proofs, these are very common in computing research and most research papers (even in systems areas like networking and programming languages) include several proofs.
What is the best internship and extra-curricular programs relating to computer science that you would recommend?
There are lots of great opportunities at UVA. I’ve been impressed with HackCville and the Computer and Network Security Club is great.

Away from Charlottesvile, the Recurse Center is very cool (when I visited it was called Hacker School), and they have students for summer sessions.

Lots of students have great experiences doing research over the summer, and there are many ways for students to get involved in research groups and have paid positions over the summer (including in mine).

I don’t want to mention specific companies for internships publicly here, but there are some that I’ve heard students have great experiences at, and other where the experiences are more mixed. I’m happy to share my thoughts on this privately during office hours (or make an appointment to meet some other time).

Do you like turtles?
Absolutely! Its turtles all the way down.
How well have your past students performed in this course? I will admit that Day 1 was a bit intimidating for me.
I haven’t taught this course before, but in general students work hard in my classes and hopefully learn a lot, and most students in my classes end up getting As. I don’t know what the distribution will be for this class (and I don’t assign grades with a target distribution in mind), but I hope to be able to have at least 2/3rds of the class get As (or at least A-s), and the rest all get at least a B (but sometimes there is no way to justify the desired grate).
Are any of the homeworks dropped?
None are “dropped” per se, but the grades are computed with many different weightings (some of which don’t count the early homeworks heavily, and others which will only count the number of “green” star or better homeworks) and generally the weighting that make your performance look best is the one that will determine your grade. All the homeworks as important for learning the material well, but you shouldn’t be stressed out about getting a low grade on one or two homeworks.

Anonymous Feedback Comments (Mon, 19 Sep 2016)

This anonymous comment was submitted through collab:

Hello Professor!

I have never been very strong at math, and whenever I take a math class I have to try very hard to keep up. This class has been the first time I have ever done a proof and I am having difficulty even getting a grasp of even the basics of this material. Would it be possible to work through more example problems in class in order to get an idea of how to apply these concepts? Also, I have sometimes have difficulty following the symbols that are used when you write in mathematical notation, would it be possible to explain some of the more complex symbols, or go a bit slower when writing them?

Thanks!

I understand what you are saying, and do appreciate the comment.

First, on the notations. If I use a notation that is unfamiliar, please stop and ask for me to define it, or at least post on slack #inclass so someone else will notice and clarify it. Notations are meant to be a convenient and compact way to write things down, and should be obfuscating the content.

On the example problems, I think you are right that we should spend a bit more time in lecture going through examples, but I also think large-scale lectures like we have for this class are just about the worst possible medium for doing this kind of technical work. (I mostly agree with Robert Talbert’s description of Four things lecture is good for and that lectures are a terrible way to cover material and transfer information.)

The reason large-scale lectures are such a bad format for going through technical examples and learning from them is that the way to learn from examples is to understand each step by figuring it out yourself, with the right leading questions to get you to that step. And, problems don’t have just one way of solving them, so you don’t want to go through a pre-set sequence of steps, but find a path to a solution that makes most sense for whoever is working on it. Spending lecture time going through techincal examples inevitably will be boring for a significant fraction of the class (that could already solve that problem on their own), and will be bewildering for some other fraction of the class (that misses some step in the explanation or is thinking about the problem in some other way). The best way to learn from examples is to go through them in very small groups (ideally one-on-one), where everyone can understand and contribute to each step. The next best way is to read examples at your own pace. Going through written examples has the benefit that everyone can go through at their own pace, and go back over steps that didn’t make sense, and then try to work out the solution on their own. (The disadvantage is that if what is written doesn’t cover some path that you are thinking about, or doesn’t explain something that is unclear, then there is no way to get more information from the static page.)

The book (at least in my view) does do a great job with most example problems, and has many good examples. As I mentioned before, my assumption is that if no one asks questions about content, including examples, in the book, that means that everyone understood it and it is not worthwhile to spend time in lecture repeating material you already understand.

Similarly, I expect everyone to read through the provided solutions to the problem sets, which I hope are clear and understandable, but you should ask questions if not. Even if you did well on an assignment, it should be worthwhile to read through the solutions, which often provide more depth or different approaches to solving problems.

So, the best thing to do is to come to office hours to go through examples in person. Next, to ask questions about examples from the book or problems on the problem sets that are unclear, and then I’ll go through those in class.

That said, I do appreciate that it will sometimes be useful to go through more basic examples in class, and will try and do this more, but balance it with my goals of making class interesting and worthwhile for people who are able to understand the text on their own.

Problem Set 2 Comments (Mon, 19 Sep 2016)

The solutions and comments for PS2 are now posted in collab: PDF

The grades will be released soon. The grading scale for PS2 is similar to what was used for PS1 (there is no “out of” goal, or “maximum” score), but scores are intended to reflect whether or not you got what was intended out of the assignment (or did better than those expectations). See the Problem Set 1 Comments for the meaning of different scores.

Problem Set 4 (Fri, 16 Sep 2016)

Problem Set 4 is now posted, and is due on Friday, 23 September at 6:29pm.